Student's t-test in R and by hand: how to compare two groups under different scenarios?
- Introduction
- Null and alternative hypothesis
- Hypothesis testing
- Different versions of the Student’s t-test
- How to compute Student’s t-test by hand?
- Scenario 1: Independent samples with 2 known variances
- Scenario 2: Independent samples with 2 equal but unknown variances
- Scenario 3: Independent samples with 2 unequal and unknown variances
- Scenario 4: Paired samples where the variance of the differences is known
- Scenario 5: Paired samples where the variance of the differences is unknown
- How to compute Student’s t-test in R?
- Scenario 1: Independent samples with 2 known variances
- Scenario 2: Independent samples with 2 equal but unknown variances
- Scenario 3: Independent samples with 2 unequal and unknown variances
- Scenario 4: Paired samples where the variance of the differences is known
- Scenario 5: Paired samples where the variance of the differences is unknown
- Combination of plot and statistical test
- Assumptions
- Conclusion
- References

Introduction
One of the most important test within the branch of inferential statistics is the Student’s t-test.1 The Student’s t-test for two samples is used to test whether two groups (two populations) are different in terms of a quantitative variable, based on the comparison of two samples drawn from these two groups. In other words, a Student’s t-test for two samples allows to determine whether the two populations from which your two samples are drawn are different (with the two samples being measured on a quantitative continuous variable).2
The reasoning behind this statistical test is that if your two samples are markedly different from each other, it can be assumed that the two populations from which the samples are drawn are different. On the contrary, if the two samples are rather similar, we cannot reject the hypothesis that the two populations are similar, so there is no sufficient evidence in the data at hand to conclude that the two populations from which the samples are drawn are different. Note that this statistical tool belongs to the branch of inferential statistics because conclusions drawn from the study of the samples are generalized to the population, even though we do not have the data on the entire population.
To compare two samples, it is usual to compare a measure of central tendency computed for each sample. In the case of the Student’s t-test, the mean is used to compare the two samples. However, in some cases, the mean is not appropriate to compare two samples so the median is used to compare them via the Wilcoxon test. This article being already quite long and complete, the Wilcoxon test is covered in a separate article, together with some illustrations on when to use one test or the other.
These two tests (Student’s t-test and Wilcoxon test) have the same final goal, that is, compare two samples in order to determine whether the two populations from which they were drawn are different or not. Note that the Student’s t-test is more powerful than the Wilcoxon test (i.e., it more often detects a significant difference if there is a true difference, so a smaller difference can be detected with the Student’s t-test) but the Student’s t-test is sensitive to outliers and data asymmetry. Furthermore, within each of these two tests, several versions exist, with each version using different formulas to arrive at the final result. It is thus necessary to understand the difference between the two tests and which version to use in order to carry out the appropriate analyses depending on the question and the data at hand.
In this article, I will first detail step by step how to perform all versions of the Student’s t-test for independent and paired samples by hand. The analyses will be done on a small set of observations for the sake of illustration and easiness. I will then show how to perform this test in R with the exact same data in order to verify the results found by hand. Reminders about the reasoning behind hypothesis testing, interpretations of the p-value and the results, and assumptions of this test will also be presented.
Note that the aim of this article is to show how to compute the Student’s t-test by hand and in R, so we refrain from testing the assumptions and we assume all of them are met for this exercise. For completeness, we still mention the assumptions, how to test them and what other tests exist if one is not met. Interested readers are invited to have a look at the end of the article for more information about these assumptions.
Null and alternative hypothesis
Before diving into the computations of the Student’s t-test by hand, let’s recap the null and alternative hypotheses of this test:
- \(H_0\): \(\mu_1 = \mu_2\)
- \(H_1\): \(\mu_1 \ne \mu_2\)
where \(\mu_1\) and \(\mu_2\) are the means of the two populations from which the samples were drawn.
As mentioned in the introduction, although technically the Student’s t-test is based on the comparison of the means of the two samples, the final goal of this test is actually to test the following hypotheses:
- \(H_0\): the two populations are similar
- \(H_1\): the two populations are different
This is in the general case where we simply want to determine whether the two populations are different or not (in terms of the dependent variable). In this sense, we have no prior belief about a particular population mean being larger or smaller than the other. This type of test is referred as a two-sided or bilateral test.
If we have some prior beliefs about one population mean being larger or smaller than the other, the Student’s t-test also allows to test the following hypotheses:
- \(H_0\): \(\mu_1 = \mu_2\)
- \(H_1\): \(\mu_1 > \mu_2\)
or
- \(H_0\): \(\mu_1 = \mu_2\)
- \(H_1\): \(\mu_1 < \mu_2\)
In the first case, we want to test if the mean of the first population is significantly larger than the mean of the second, while in the latter case, we want to test if the mean of the first population is significantly smaller than the mean of the second. This type of test is referred as a one-sided or unilateral test.
Some authors argue that one-sided tests should not be used in practice for the simple reason that, if a researcher is so sure that the mean of one population is larger (smaller) than the mean of the other and would never be smaller (larger) than the other, why would she needs to test for significance at all? This a rather philosophical question and it is beyond the scope of this article. Interested readers are invited to see part of the discussion in Rowntree (2000).
Hypothesis testing
In statistics, many statistical tests is in the form of hypothesis tests. Hypothesis tests are used to determine whether a certain belief can be deemed as true (plausible) or not, based on the data at hand (i.e., the sample(s)). Most hypothesis tests boil down to the following 4 steps:3
- State the null and alternative hypothesis.
- Compute the test statistic, denoted t-stat. Formulas to compute the test statistic differ among the different versions of the Student’s t-test but they have the same structure. See scenarios 1 to 5 below to see the different formulas.
- Find the critical value given the theoretical statistical distribution of the test, the parameters of the distribution and the significance level \(\alpha\). For a Student’s t-test and its extended version, it is either the normal or the Student’s t distribution (t denoting the Student distribution and z denoting the normal distribution).
- Conclude by comparing the t-stat (found in step 2.) with the critical value (found in step. 3). If the t-stat lies in the rejection region (determined thanks to the critical value and the direction of the test), we reject the null hypothesis, otherwise we do not reject the null hypothesis. These two alternatives (reject or do not reject the null hypothesis) are the only two possible solutions, we never “accept” an hypothesis. It is also a good practice to always interpret the decision in the terms of the initial question.
For the interested reader, see these 4 steps of hypothesis testing in more details in this article.
Different versions of the Student’s t-test
There are several versions of the Student’s t-test for two samples, depending on whether the samples are independent or paired and depending on whether the variances of the populations are (un)equal and/or (un)known:
On the one hand, independent samples means that the two samples are collected on different experimental units or different individuals, for instance when we are working on women and men separately, or working on patients who have been randomly assigned to a control and a treatment group (and a patient belongs to only one group). On the other hand, we face paired samples when measurements are collected on the same experimental units, same individuals. This is often the case, for example in medical studies, when testing the efficiency of a treatment at two different times. The same patients are measured twice, before and after the treatment, and the dependency between the two samples must be taken into account in the computation of the test statistic by working on the differences of measurements for each subject. Paired samples are usually the result of measurements at two different times, but not exclusively. Suppose we want to test the difference in vision between the left and right eyes of 50 athletes. Although the measurements are not made at two different time (before-after), it is clear that both eyes are dependent within each subject. Therefore, the Student’s t-test for paired samples should be used to account for the dependency between the two samples instead of the standard Student’s t-test for independent samples.
Another criteria for choosing the appropriate version of the Student’s t-test is whether the variances of the populations (not the variances of the samples!) are known or unknown and equal or unequal. This criteria is rather straightforward, we either know the variances of the populations or we do not. The variances of the populations cannot be computed because if you can compute the variance of a population, it means you have the data for the whole population, then there is no need to do a hypothesis test anymore… So the variances of the populations are either given in the statement (use them in that case), or there is no information about these variances and in this case, it is assumed that the variances are unknown. In practice, the variances of the populations are most of the time unknown and the only thing to do in order to choose the appropriate version of the test is to check whether the variances are equal or not. However, we still illustrate how to do all versions of this test by hand and in R in the next sections following the 4 steps of hypothesis testing.
How to compute Student’s t-test by hand?
Note that the data are artificial and do not represent any real variable. Furthermore, remind that the assumptions may or may not be met. The point of the article is to detail how to compute the different versions of the test by hand and in R, so all assumptions are assumed to be met. Moreover, assume that the significance level \(\alpha = 5\)% for all tests.
If you are interested in applying these tests by hand without having to do the computations yourself, here is a Shiny app which does it for you. You just need to enter the data and choose the appropriate version of the test thanks to the sidebar menu. There is also a graphical representation that helps you to visualize the test statistic and the rejection region. I hope you will find it useful!
Scenario 1: Independent samples with 2 known variances
For the first scenario, suppose the data below. Moreover, suppose that the two samples are independent, that the variances \(\sigma^2 = 1\) in both populations and that we would like to test whether the two population means are different.
| value | sample |
|---|---|
| 0.9 | 1 |
| -0.8 | 1 |
| 0.1 | 1 |
| -0.3 | 1 |
| 0.2 | 1 |
| 0.8 | 2 |
| -0.9 | 2 |
| -0.1 | 2 |
| 0.4 | 2 |
| 0.1 | 2 |
So we have:
- 5 observations in each sample: \(n_1 = n_2 = 5\)
- mean of sample 1: \(\bar{x}_1 = 0.02\)
- mean of sample 2: \(\bar{x}_2 = 0.06\)
- variances of both populations: \(\sigma^2_1 = \sigma^2_2 = 1\)
Following the 4 steps of hypothesis testing we have:
- \(H_0: \mu_1 = \mu_2\) and \(H_1: \mu_1 - \mu_2 \ne 0\). (\(\ne\) because we want to test whether the two means are different, we do not impose a direction in the test.)
- Test statistic: \[z_{obs} = \frac{(\bar{x}_1 - \bar{x}_2) - (\mu_1 - \mu_2)}{\sqrt{\frac{\sigma^2_1}{n_1} + \frac{\sigma^2_2}{n_2}}}\] \[= \frac{0.02-0.06-0}{0.632} = -0.063\]
- Critical value: \(\pm z_{\alpha / 2} = \pm z_{0.025} = \pm 1.96\) (see a guide on how to read statistical tables if you struggle to find the critical value)
- Conclusion: The rejection regions are thus from \(-\infty\) to -1.96 and from 1.96 to \(+\infty\). The test statistic is outside the rejection regions so we do not reject the null hypothesis \(H_0\). In terms of the initial question: At the 5% significance level, we do not reject the hypothesis that the two population means are the same, or there is no sufficient evidence in the data to conclude that the two populations considered are different.
Scenario 2: Independent samples with 2 equal but unknown variances
For the second scenario, suppose the data below. Moreover, suppose that the two samples are independent, that the variances in both populations are unknown but equal (\(\sigma^2_1 = \sigma^2_1\)) and that we would like to test whether the mean of population 1 is larger than the mean of population 2.
| value | sample |
|---|---|
| 1.78 | 1 |
| 1.5 | 1 |
| 0.9 | 1 |
| 0.6 | 1 |
| 0.8 | 1 |
| 1.9 | 1 |
| 0.8 | 2 |
| -0.7 | 2 |
| -0.1 | 2 |
| 0.4 | 2 |
| 0.1 | 2 |
So we have:
- 6 observations in sample 1: \(n_1 = 6\)
- 5 observations in sample 2: \(n_2 = 5\)
- mean of sample 1: \(\bar{x}_1 = 1.247\)
- mean of sample 2: \(\bar{x}_2 = 0.1\)
- variance of sample 1: \(s^2_1 = 0.303\)
- variance of sample 2: \(s^2_1 = 0.315\)
Following the 4 steps of hypothesis testing we have:
- \(H_0: \mu_1 = \mu_2\) and \(H_1: \mu_1 - \mu_2 > 0\). (> because we want to test if the mean of the first population is larger than the mean of the second population.)
- Test statistic: \[t_{obs} = \frac{(\bar{x}_1 - \bar{x}_2) - (\mu_1 - \mu_2)}{s_p\sqrt{\frac{1}{n_1} + \frac{1}{n_2}}}\] where \[s_p = \sqrt{\frac{(n_1-1)s^2_1+ (n_2 - 1)s^2_2}{n_1 + n_2 - 2}} = 0.555\] so \[t_{obs} = \frac{1.247-0.1-0}{0.555 * 0.606} = 3.411\] (Note that as it is assumed the variances of the two populations are equal, a pooled (common) variance, denoted \(s_p\), is computed.)
- Critical value: \(t_{\alpha, n_1 + n_2 - 2} = t_{0.05, 9} = 1.833\)
- Conclusion: The rejection region is thus from 1.833 to \(+\infty\) (there is only one rejection region because it is a one-sided test). The test statistic lies within the rejection region so we reject the null hypothesis \(H_0\). In terms of the initial question: At the 5% significance level, we conclude that the mean of population 1 is larger than the mean of population 2.
Scenario 3: Independent samples with 2 unequal and unknown variances
For the third scenario, suppose the data below. Moreover, suppose that the two samples are independent, that the variances in both populations are unknown and unequal (\(\sigma^2_1 \ne \sigma^2_1\)) and that we would like to test whether the mean of population 1 is smaller than the mean of population 2.
| value | sample |
|---|---|
| 0.8 | 1 |
| 0.7 | 1 |
| 0.1 | 1 |
| 0.4 | 1 |
| 0.1 | 1 |
| 1.78 | 2 |
| 1.5 | 2 |
| 0.9 | 2 |
| 0.6 | 2 |
| 0.8 | 2 |
| 1.9 | 2 |
So we have:
- 5 observations in sample 1: \(n_1 = 5\)
- 6 observations in sample 2: \(n_2 = 6\)
- mean of sample 1: \(\bar{x}_1 = 0.42\)
- mean of sample 2: \(\bar{x}_2 = 1.247\)
- variance of sample 1: \(s^2_1 = 0.107\)
- variance of sample 2: \(s^2_1 = 0.303\)
Following the 4 steps of hypothesis testing we have:
- \(H_0: \mu_1 = \mu_2\) and \(H_1: \mu_1 - \mu_2 < 0\). (< because we want to test if the mean of the first population is smaller than the mean of the second population.)
- Test statistic: \[t_{obs} = \frac{(\bar{x}_1 - \bar{x}_2) - (\mu_1 - \mu_2)}{\sqrt{\frac{s^2_1}{n_1} + \frac{s^2_2}{n_2}}}\] \[= \frac{0.42-1.247-0}{0.268} = -3.084\]
- Critical value: \(-t_{\alpha, \upsilon}\) where \[\upsilon = \frac{\bigg(\frac{s^2_1}{n_1} + \frac{s^2_2}{n_2} \bigg)^2}{\frac{\bigg(\frac{s^2_1}{n_1}\bigg)^2}{n_1 - 1} + \frac{\bigg(\frac{s^2_2}{n_2}\bigg)^2}{n_2 - 1}} = 8.28\] so \[-t_{0.05, 8.28} = -1.851\]
Note: The degrees of freedom 8.28 does not exist in the standard Student distribution table, so simply take 8, or compute it in R with
qt(p = 0.05, df = 8.28). For simplicity, this number of degrees of freedom is sometimes approximated as \(df = min(n_1 - 1, n_2 - 1)\), so in this case it would be \(df = 4\). - Conclusion: The rejection region is thus from \(-\infty\) to -1.851. The test statistic lies within the rejection region so we reject the null hypothesis \(H_0\). In terms of the initial question: At the 5% significance level, we conclude that the mean of population 1 is smaller than the mean of population 2.
Scenario 4: Paired samples where the variance of the differences is known
Student’s t-test with paired samples are a bit different than with independent samples, they are actually more similar to one sample Student’s t-test. Here is how it works. We actually compute the difference between the two samples for each pair of observations, and then we work on these differences as if we were doing a one sample Student’s t-test by computing the test statistic on these differences.
In case it is not clear, here is the fourth scenario as an illustration. Suppose the data below. Moreover, suppose that the two samples are dependent (matched), that the variance of the differences in the population is known and equal to 1 (\(\sigma^2_D = 1\)) and that we would like to test whether the mean difference between the two populations is different than 0.
| before | after |
|---|---|
| 0.9 | 0.8 |
| -0.8 | -0.9 |
| 0.1 | -0.1 |
| -0.3 | 0.4 |
| 0.2 | 0.1 |
The first thing to do is to compute the differences for all pairs of observations:
| before | after | difference |
|---|---|---|
| 0.9 | 0.8 | -0.1 |
| -0.8 | -0.9 | -0.1 |
| 0.1 | -0.1 | -0.2 |
| -0.3 | 0.4 | 0.7 |
| 0.2 | 0.1 | -0.1 |
So we have:
- number of pairs: \(n = 5\)
- mean of the difference: \(\bar{D} = 0.04\)
- variance of the difference in the population: \(\sigma^2_D = 1\)
- standard deviation of the difference in the population: \(\sigma_D = 1\)
Following the 4 steps of hypothesis testing we have:
- \(H_0: \mu_D = 0\) and \(H_1: \mu_D \ne 0\)
- Test statistic: \[z_{obs} = \frac{\bar{D} - \mu_0}{\frac{\sigma_D}{\sqrt{n}}} = \frac{0.04-0}{0.447} = 0.089\] (This formula is exactly the same than for one sample Student’s t-test with a known variance, except that we work on the mean of the differences.)
- Critical value: \(\pm z_{\alpha/2} = \pm z_{0.025} = \pm 1.96\)
- Conclusion: The rejection regions are thus from \(-\infty\) to -1.96 and from 1.96 to \(+\infty\). The test statistic is outside the rejection regions so we do not reject the null hypothesis \(H_0\). In terms of the initial question: At the 5% significance level, we do not reject the hypothesis that the mean difference between the two populations is equal to 0.
Scenario 5: Paired samples where the variance of the differences is unknown
For the fifth and final scenario, suppose the data below. Moreover, suppose that the two samples are dependent (matched), that the variance of the differences in the population is unknown and that we would like to test whether a treatment is effective in increasing running capabilities (the higher the value, the better in terms of running capabilities).
| before | after |
|---|---|
| 9 | 16 |
| 8 | 11 |
| 1 | 15 |
| 3 | 12 |
| 2 | 9 |
The first thing to do is to compute the differences for all pairs of observations:
| before | after | difference |
|---|---|---|
| 9 | 16 | 7 |
| 8 | 11 | 3 |
| 1 | 15 | 14 |
| 3 | 12 | 9 |
| 2 | 9 | 7 |
So we have:
- number of pairs: \(n = 5\)
- mean of the difference: \(\bar{D} = 8\)
- variance of the difference in the sample: \(s^2_D = 16\)
- standard deviation of the difference in the sample: \(s_D = 4\)
Following the 4 steps of hypothesis testing we have:
- \(H_0: \mu_D = 0\) and \(H_1: \mu_D > 0\) (> because we would like to test whether the treatment is effective, so whether the treatment has a positive impact on the running capabilities.)
- Test statistic: \[t_{obs} = \frac{\bar{D} - \mu_0}{\frac{s_D}{\sqrt{n}}} = \frac{8-0}{1.789} = 4.472\] (This formula is exactly the same than for one sample Student’s t-test with an unknown variance, except that we work on the mean of the differences.)
- Critical value: \(t_{\alpha, n-1} = t_{0.05, 4} = 2.132\) (n is the number of pairs, not the number of observations!)
- Conclusion: The rejection regions are thus from 2.132 to \(+\infty\). The test statistic lies within the rejection region so we reject the null hypothesis \(H_0\). In terms of the initial question: At the 5% significance level, we conclude that the treatment has a positive impact on the running capabilities (because the mean of the differences is greater than 0)
This concludes how to perform the different versions of the Student’s t-test for two samples by hand. In the next sections, we detail how to perform the exact same tests in R.
How to compute Student’s t-test in R?
A good practice before doing t-tests in R is to visualize the data by group thanks to a boxplot (or a density plot, or eventually both). A boxplot with the two boxes overlapping each other gives a first indication that the two samples are similar, and thus, that the null hypothesis of equal means may not be rejected. On the contrary, if the two boxes are not overlapping, it indicates that the two samples are not similar, and thus, that the populations may be different in terms of the considered variable. However, even if boxplots or density plots are great in showing a comparison between the two groups, only a sound statistical test will confirm our first impression.
After a visualization of the data by group, we replicate in R the results found by hand. We will see that for some versions of the t-test, there is no default function built in R (at least to my knowledge, do not hesitate to let me know in the comments if I’m mistaken). In these cases, a function is written to replicate the results by hand.
Note that we use the same data, the same assumptions and the same question for all 5 scenarios to facilitate the comparison between the tests performed by hand and in R.
Scenario 1: Independent samples with 2 known variances
For the first scenario, suppose the data below. Moreover, suppose that the two samples are independent, that the variances \(\sigma^2 = 1\) in both populations and that we would like to test whether the two population means are different.
dat1 <- data.frame(
sample1 = c(0.9, -0.8, 0.1, -0.3, 0.2),
sample2 = c(0.8, -0.9, -0.1, 0.4, 0.1)
)
dat1## sample1 sample2
## 1 0.9 0.8
## 2 -0.8 -0.9
## 3 0.1 -0.1
## 4 -0.3 0.4
## 5 0.2 0.1dat_ggplot <- data.frame(
value = c(0.9, -0.8, 0.1, -0.3, 0.2, 0.8, -0.9, -0.1, 0.4, 0.1),
sample = c(rep("1", 5), rep("2", 5))
)
library(ggplot2)
ggplot(dat_ggplot) +
aes(x = sample, y = value) +
geom_boxplot() +
theme_minimal()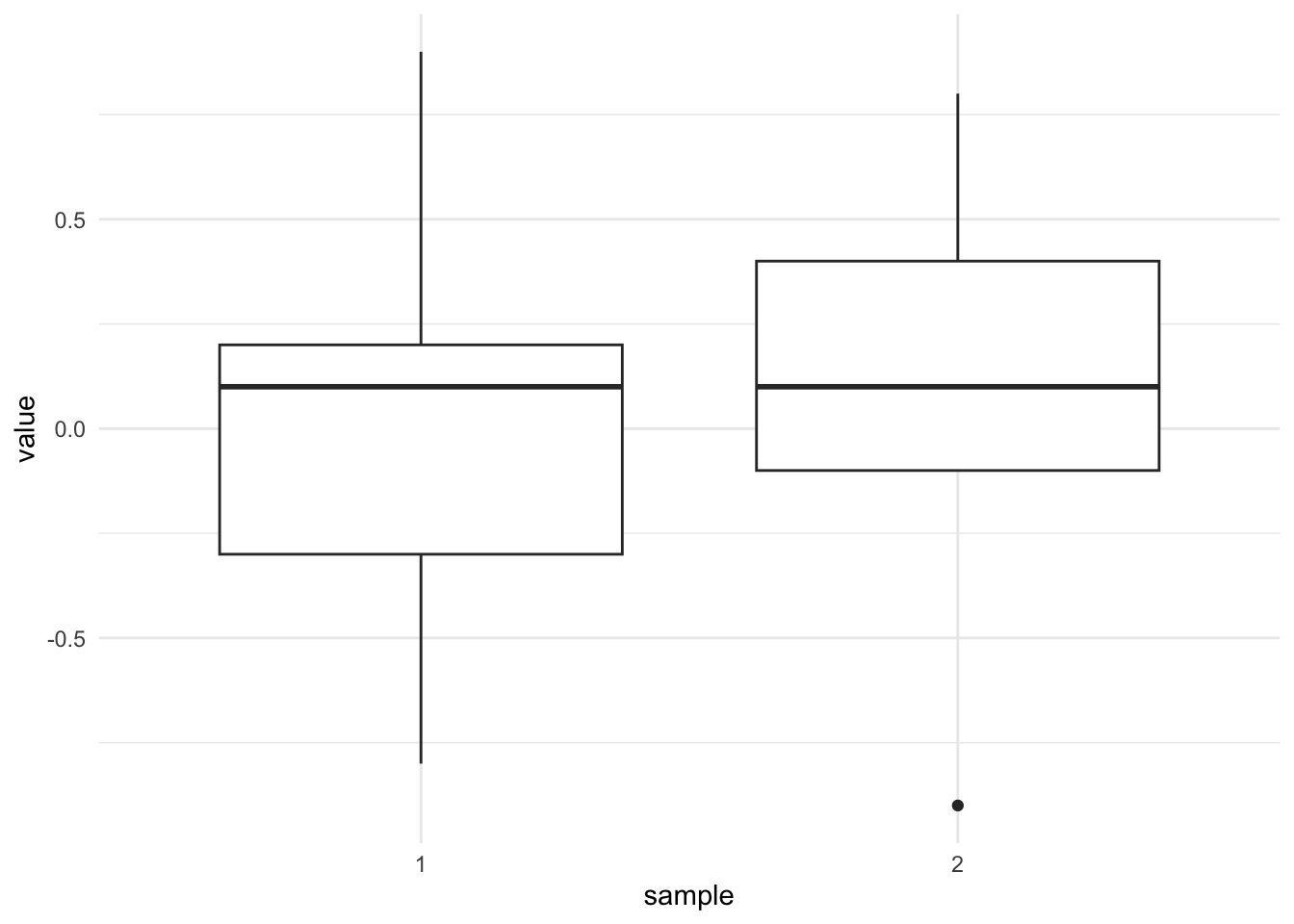
Note that you can use the {esquisse} RStudio addin if you want to draw a boxplot with the package {ggplot2} without writing the code yourself. If you prefer the default graphics, use the boxplot() function:
boxplot(value ~ sample,
data = dat_ggplot
)
The two boxes seem to overlap which illustrate that the two samples are quite similar, so we tend to believe that we will not be able to reject the null hypothesis that the two population means are similar. However, only a formal statistical test will confirm this belief.
Below a function to perform a t-test with known variances, with arguments accepting:
- the two samples (
xandy), - the two variances of the populations (
V1andV2), - the difference in means under the null hypothesis (
m0, default is0), - the significance level (
alpha, default is0.05) - and the alternative (
alternative, one of"two.sided"(default),"less"or"greater"):
t.test_knownvar <- function(x, y, V1, V2, m0 = 0, alpha = 0.05, alternative = "two.sided") {
M1 <- mean(x)
M2 <- mean(y)
n1 <- length(x)
n2 <- length(y)
sigma1 <- sqrt(V1)
sigma2 <- sqrt(V2)
S <- sqrt((V1 / n1) + (V2 / n2))
statistic <- (M1 - M2 - m0) / S
p <- if (alternative == "two.sided") {
2 * pnorm(abs(statistic), lower.tail = FALSE)
} else if (alternative == "less") {
pnorm(statistic, lower.tail = TRUE)
} else {
pnorm(statistic, lower.tail = FALSE)
}
LCL <- (M1 - M2 - S * qnorm(1 - alpha / 2))
UCL <- (M1 - M2 + S * qnorm(1 - alpha / 2))
value <- list(mean1 = M1, mean2 = M2, m0 = m0, sigma1 = sigma1, sigma2 = sigma2, S = S, statistic = statistic, p.value = p, LCL = LCL, UCL = UCL, alternative = alternative)
# print(sprintf("P-value = %g",p))
# print(sprintf("Lower %.2f%% Confidence Limit = %g",
# alpha, LCL))
# print(sprintf("Upper %.2f%% Confidence Limit = %g",
# alpha, UCL))
return(value)
}
test <- t.test_knownvar(dat1$sample1, dat1$sample2,
V1 = 1, V2 = 1
)
test## $mean1
## [1] 0.02
##
## $mean2
## [1] 0.06
##
## $m0
## [1] 0
##
## $sigma1
## [1] 1
##
## $sigma2
## [1] 1
##
## $S
## [1] 0.6324555
##
## $statistic
## [1] -0.06324555
##
## $p.value
## [1] 0.949571
##
## $LCL
## [1] -1.27959
##
## $UCL
## [1] 1.19959
##
## $alternative
## [1] "two.sided"The output above recaps all the information needed to perform the test: the test statistic, the p-value, the alternative used, the two sample means and the two variances of the populations (compare these results found in R with the results found by hand).
The p-value can be extracted as usual:
test$p.value## [1] 0.949571The p-value is 0.95 so at the 5% significance level we do not reject the null hypothesis of equal means. There is no sufficient evidence in the data to reject the hypothesis that the two means in the populations are similar. This result confirms what we found by hand.
Note that a similar function exists in the {BSDA} package:4
library(BSDA)
z.test(dat1$sample1,
dat1$sample2,
alternative = "two.sided",
mu = 0,
sigma.x = 1,
sigma.y = 1,
conf.level = 0.95
)##
## Two-sample z-Test
##
## data: dat1$sample1 and dat1$sample2
## z = -0.063246, p-value = 0.9496
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
## -1.27959 1.19959
## sample estimates:
## mean of x mean of y
## 0.02 0.06A note on p-value and significance level \(\alpha\)
For those unfamiliar with the concept of p-value, the p-value is a probability and as any probability it goes from 0 to 1. The p-value is the probability of having observations at least as extreme as the one we measured (via the samples) if the null hypothesis were true. In other words, it is the probability of having a test statistic at least as extreme as the one we computed, given that the null hypothesis is true. In some sense, it gives you an indication on how likely your null hypothesis is. It is also defined as the smallest level of significance for which the data indicate rejection of the null hypothesis.
If the observations are not so extreme—not unlikely to occur if the null hypothesis were true—we do not reject this null hypothesis because it is deemed plausible to be true. And if the observations are considered too extreme—too unlikely to happen under the null hypothesis—we reject the null hypothesis because it is deemed too implausible to be true. Note that it does not mean that we are 100% sure that it is too unlikely, it happens sometimes that the null hypothesis is rejected although it is true (see the significance level \(\alpha\) later on).
In our example above, the observations are not really extreme and the difference between the two means is not extreme, so the test statistic is not extreme (since the test statistic is partially based on the difference of the means of the two samples). Having a test statistic which is not extreme is not unlikely and that is the reason why the p-value is quite high. The p-value of 0.95 actually tells us that the probability of having two samples with a difference in means of -0.04 (= 0.02 - 0.06), given that the difference in means in the populations is 0 (the null hypothesis), equals 95%. A probability of 95% is definitely considered as plausible, so we do not reject the null hypothesis of equal means in the populations.
One may then wonder, “What is too extreme for a test statistic?” Most of the time, we consider that a test statistic is too extreme to happen just by chance when the probability of having such an extreme test statistic given that the null hypothesis is true is below 5%. The threshold of 5% (\(\alpha = 0.05\)) that you very often see in statistic courses or textbooks is the threshold used in many fields. With a p-value under that threshold of 5%, we consider that the observations (and thus the test statistic) is too unlikely to happen just by chance if the null hypothesis were true, so the null hypothesis is rejected. With a p-value above that threshold of 5%, we consider that it is not really implausible to face the observations we have if the null hypothesis were true, and we therefore do not reject the null hypothesis.
Note that I wrote “we do not reject the null hypothesis”, and not “we accept the null hypothesis”. This is because it may be the case that the null hypothesis is in fact false, but we failed to prove it with the samples. Suppose the analogy of a suspect accused of murder and we do not know the truth. On the one hand, if we have collected enough evidence that the suspect committed the murder, he is considered guilty: we reject the null hypothesis that he is innocent. On the other hand, if we have not collected enough evidence against the suspect, he is presumed to be innocent although he may in fact have committed the crime: we failed to reject the null hypothesis of him being innocent. We are never sure that he did not commit the crime even if he is released, we just did not find sufficient evidence against the null hypothesis of the suspect being innocent. This is the reason why we do not reject the null hypothesis instead of accepting it, and why you will often read things like “there is no sufficient evidence in the data to reject the null hypothesis” or “based on the samples we fail to reject the null hypothesis”.
The significance level \(\alpha\), derived from the threshold of 5% mentioned earlier, is the probability of rejecting the null hypothesis when it is in fact true. In this sense, it is an error (of 5%) that we accept to deal with, in order to be able to draw conclusions. If we would accept no error (an error of 0%), we would not be able to draw any conclusion about the population(s) since we only have access to a limited portion of the population(s) via the sample(s). As a consequence, we will never be 100% sure when interpreting the result of a hypothesis test unless we have access to the data for the entire population, but then there is no reason to do a hypothesis test anymore since we can simply compare the two populations. We usually allow this error (called Type I error) to be 5%, but in order to be a bit more certain when concluding that we reject the null hypothesis, the alpha level can also be set to 1% (or even to 0.1% in some rare cases).
To sum up what you need to remember about p-value and significance level \(\alpha\):
- If the p-value is smaller than the predetermined significance level \(\alpha\) (usually 5%) so if p-value < 0.05 \(\rightarrow H_0\) is unlikely \(\rightarrow\) we reject the null hypothesis
- If the p-value is greater than or equal to the predetermined significance level \(\alpha\) (usually 5%) so if p-value \(\ge\) 0.05 \(\rightarrow H_0\) is likely \(\rightarrow\) we do not reject the null hypothesis
This applies to all statistical tests without exception. Of course, the null and alternative hypotheses change depending on the test.
A rule of thumb is that, for most hypothesis tests, the alternative hypothesis is what you want to test and the null hypothesis is the status quo. Take this with extreme caution (!) because, even if it works for all versions of the Student’s t-test it does not apply to ALL statistical tests. For example, when testing for normality, you usually want to test whether your distribution follows a normal distribution. Following this piece of advice, you would write the alternative hypothesis \(H_1:\) the distribution follows a normal distribution. Nonetheless, for normality tests such as the Shapiro-Wilk or Kolmogorov-Smirnov test, it is the opposite; the alternative hypothesis is \(H_1:\) the distribution does not follow a normal distribution. So for every test, make sure to use the correct hypotheses, otherwise the conclusion and interpretation of your test will be wrong.
Last but not least, note that statistical significance is not equal to scientific significance. To this end, a result may be statistically significant (a p-value < \(\alpha\)), but of little or no interest from a scientific point of view (because the effect is so small that it is negligible and/or useless for instance).
Scenario 2: Independent samples with 2 equal but unknown variances
For the second scenario, suppose the data below. Moreover, suppose that the two samples are independent, that the variances in both populations are unknown but equal (\(\sigma^2_1 = \sigma^2_1\)) and that we would like to test whether the mean of population 1 is larger than the mean of population 2.
dat2 <- data.frame(
sample1 = c(1.78, 1.5, 0.9, 0.6, 0.8, 1.9),
sample2 = c(0.8, -0.7, -0.1, 0.4, 0.1, NA)
)
dat2## sample1 sample2
## 1 1.78 0.8
## 2 1.50 -0.7
## 3 0.90 -0.1
## 4 0.60 0.4
## 5 0.80 0.1
## 6 1.90 NAdat_ggplot <- data.frame(
value = c(1.78, 1.5, 0.9, 0.6, 0.8, 1.9, 0.8, -0.7, -0.1, 0.4, 0.1),
sample = c(rep("1", 6), rep("2", 5))
)
ggplot(dat_ggplot) +
aes(x = sample, y = value) +
geom_boxplot() +
theme_minimal()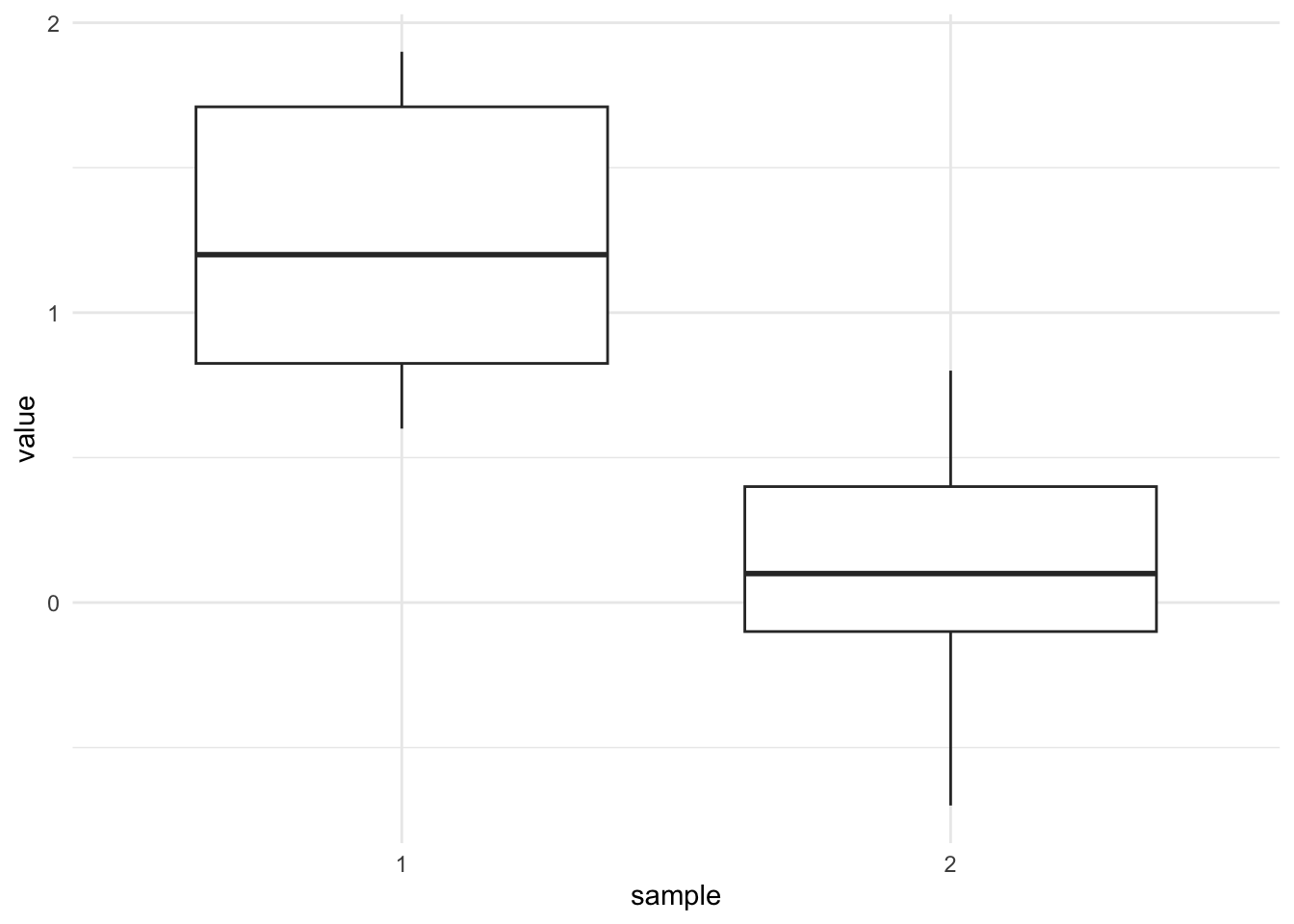
Unlike the previous scenario, the two boxes do not overlap which illustrates that the two samples are different from each other. From this boxplot, we can expect the test to reject the null hypothesis of equal means in the populations. Nonetheless, only a formal statistical test will confirm this expectation.
There is a function in R, and it is simply the t.test() function. This version of the test is actually the “standard” Student’s t-test for two samples. Note that it is assumed that the variances of the two populations are equal so we need to specify it in the function with the argument var.equal = TRUE (the default is FALSE) and the alternative hypothesis is \(H_1: \mu_1 - \mu_2 > 0\) so we need to add the argument alternative = "greater" as well:
test <- t.test(dat2$sample1, dat2$sample2,
var.equal = TRUE, alternative = "greater"
)
test##
## Two Sample t-test
##
## data: dat2$sample1 and dat2$sample2
## t = 3.4113, df = 9, p-value = 0.003867
## alternative hypothesis: true difference in means is greater than 0
## 95 percent confidence interval:
## 0.5304908 Inf
## sample estimates:
## mean of x mean of y
## 1.246667 0.100000The output above recaps all the information needed to perform the test: the name of the test, the test statistic, the degrees of freedom, the p-value, the alternative used and the two sample means (compare these results found in R with the results found by hand).
The p-value can be extracted as usual:
test$p.value## [1] 0.003866756The p-value is 0.004 so at the 5% significance level we reject the null hypothesis of equal means. This result confirms what we found by hand.
Unlike the first scenario, the p-value in this scenario is below 5% so we reject the null hypothesis. At the 5% significance level, we can conclude that the mean of population 1 is larger than the mean of population 2.
A nice and easy way to report results of a Student’s t-test in R is with the report() function from the {report} package:
# install.packages("remotes")
# remotes::install_github("easystats/report") # You only need to do that once
library("report") # Load the package every time you start R
report(test)## Effect sizes were labelled following Cohen's (1988) recommendations.
##
## The Two Sample t-test testing the difference between dat2$sample1 and
## dat2$sample2 (mean of x = 1.25, mean of y = 0.10) suggests that the effect is
## positive, statistically significant, and large (difference = 1.15, 95% CI
## [0.53, Inf], t(9) = 3.41, p = 0.004; Cohen's d = 2.07, 95% CI [0.75, Inf])As you can see, the function interprets the test (together with the p-value) for you.
Note that the report() function can be used for other analyses. See more tips and tricks in R if you find this one useful.
If your data is formatted in the long format (which is even better), simply use the tilde (~). For instance, imagine the exact same data presented like this:
dat2bis <- data.frame(
value = c(1.78, 1.5, 0.9, 0.6, 0.8, 1.9, 0.8, -0.7, -0.1, 0.4, 0.1),
sample = c(rep("1", 6), rep("2", 5))
)
dat2bis## value sample
## 1 1.78 1
## 2 1.50 1
## 3 0.90 1
## 4 0.60 1
## 5 0.80 1
## 6 1.90 1
## 7 0.80 2
## 8 -0.70 2
## 9 -0.10 2
## 10 0.40 2
## 11 0.10 2Here is how to perform the Student’s t-test in R with data in the long format:
test <- t.test(value ~ sample,
data = dat2bis,
var.equal = TRUE,
alternative = "greater"
)
test##
## Two Sample t-test
##
## data: value by sample
## t = 3.4113, df = 9, p-value = 0.003867
## alternative hypothesis: true difference in means between group 1 and group 2 is greater than 0
## 95 percent confidence interval:
## 0.5304908 Inf
## sample estimates:
## mean in group 1 mean in group 2
## 1.246667 0.100000test$p.value## [1] 0.003866756The results are exactly the same.
Scenario 3: Independent samples with 2 unequal and unknown variances
For the third scenario, suppose the data below. Moreover, suppose that the two samples are independent, that the variances in both populations are unknown and unequal (\(\sigma^2_1 \ne \sigma^2_1\)) and that we would like to test whether the mean of population 1 is smaller than the mean of population 2.
dat3 <- data.frame(
value = c(0.8, 0.7, 0.1, 0.4, 0.1, 1.78, 1.5, 0.9, 0.6, 0.8, 1.9),
sample = c(rep("1", 5), rep("2", 6))
)
dat3## value sample
## 1 0.80 1
## 2 0.70 1
## 3 0.10 1
## 4 0.40 1
## 5 0.10 1
## 6 1.78 2
## 7 1.50 2
## 8 0.90 2
## 9 0.60 2
## 10 0.80 2
## 11 1.90 2ggplot(dat3) +
aes(x = sample, y = value) +
geom_boxplot() +
theme_minimal()
There is a function in R for this version of the test as well, and it is simply the t.test() function with the var.equal = FALSE argument. FALSE is the default option for the var.equal argument so you actually do not need to specify it. This version of the test is actually the Welch Student’s test, used when the variances of the populations are unknown and unequal. To test if two population variances are equal, you can use the Levene’s test (leveneTest(dat3$value, dat3$sample) from the {car} package, or simply by comparing the dispersion of the two samples via a dotplot or a boxplot). Note that the alternative hypothesis is \(H_1: \mu_1 - \mu_2 < 0\) so we need to add the argument alternative = "less" as well:
test <- t.test(value ~ sample,
data = dat3,
var.equal = FALSE,
alternative = "less"
)
test##
## Welch Two Sample t-test
##
## data: value by sample
## t = -3.0841, df = 8.2796, p-value = 0.007206
## alternative hypothesis: true difference in means between group 1 and group 2 is less than 0
## 95 percent confidence interval:
## -Inf -0.3304098
## sample estimates:
## mean in group 1 mean in group 2
## 0.420000 1.246667The output above recaps all the information needed to perform the test (compare these results found in R with the results found by hand).
The p-value can be extracted as usual:
test$p.value## [1] 0.00720603The p-value is 0.007 so at the 5% significance level we reject the null hypothesis of equal means, meaning that we can conclude that the mean of population 1 is smaller than the mean of population 2. This result confirms what we found by hand.
Scenario 4: Paired samples where the variance of the differences is known
For the fourth scenario, suppose the data below. Moreover, suppose that the two samples are dependent (matched), that the variance of the differences in the population is known and equal to 1 (\(\sigma^2_D = 1\)) and that we would like to test whether the mean difference between the two populations is different than 0.
dat4 <- data.frame(
before = c(0.9, -0.8, 0.1, -0.3, 0.2),
after = c(0.8, -0.9, -0.1, 0.4, 0.1)
)
dat4## before after
## 1 0.9 0.8
## 2 -0.8 -0.9
## 3 0.1 -0.1
## 4 -0.3 0.4
## 5 0.2 0.1dat4$difference <- dat4$after - dat4$before
ggplot(dat4) +
aes(y = difference) +
geom_boxplot() +
theme_minimal()
Since there is no function in R to perform a t-test with paired samples where the variance of the differences is known, here is one with arguments accepting:
- the differences between the two samples (
x), - the variance of the differences in the population (
V), - the mean of the differences under the null hypothesis (
m0, default is0), - the significance level (
alpha, default is0.05) - and the alternative (
alternative, one of"two.sided"(default),"less"or"greater"):
t.test_pairedknownvar <- function(x, V, m0 = 0, alpha = 0.05, alternative = "two.sided") {
M <- mean(x)
n <- length(x)
sigma <- sqrt(V)
S <- sqrt(V / n)
statistic <- (M - m0) / S
p <- if (alternative == "two.sided") {
2 * pnorm(abs(statistic), lower.tail = FALSE)
} else if (alternative == "less") {
pnorm(statistic, lower.tail = TRUE)
} else {
pnorm(statistic, lower.tail = FALSE)
}
LCL <- (M - S * qnorm(1 - alpha / 2))
UCL <- (M + S * qnorm(1 - alpha / 2))
value <- list(mean = M, m0 = m0, sigma = sigma, statistic = statistic, p.value = p, LCL = LCL, UCL = UCL, alternative = alternative)
# print(sprintf("P-value = %g",p))
# print(sprintf("Lower %.2f%% Confidence Limit = %g",
# alpha, LCL))
# print(sprintf("Upper %.2f%% Confidence Limit = %g",
# alpha, UCL))
return(value)
}
test <- t.test_pairedknownvar(dat4$after - dat4$before,
V = 1
)
test## $mean
## [1] 0.04
##
## $m0
## [1] 0
##
## $sigma
## [1] 1
##
## $statistic
## [1] 0.08944272
##
## $p.value
## [1] 0.9287301
##
## $LCL
## [1] -0.8365225
##
## $UCL
## [1] 0.9165225
##
## $alternative
## [1] "two.sided"The output above recaps all the information needed to perform the test (compare these results found in R with the results found by hand).
The p-value can be extracted as usual:
test$p.value## [1] 0.9287301The p-value is 0.929 so at the 5% significance level we do not reject the null hypothesis of the mean of the differences being equal to 0. There is no sufficient evidence in the data to reject the hypothesis that the mean difference between the two populations is equal to 0. This result confirms what we found by hand.
Scenario 5: Paired samples where the variance of the differences is unknown
For the fifth and final scenario, suppose the data below. Moreover, suppose that the two samples are dependent (matched), that the variance of the differences in the population is unknown and that we would like to test whether a treatment is effective in increasing running capabilities (the higher the value, the better in terms of running capabilities).
dat5 <- data.frame(
before = c(9, 8, 1, 3, 2),
after = c(16, 11, 15, 12, 9)
)
dat5## before after
## 1 9 16
## 2 8 11
## 3 1 15
## 4 3 12
## 5 2 9dat5$difference <- dat5$after - dat5$before
ggplot(dat5) +
aes(y = difference) +
geom_boxplot() +
theme_minimal()
There is a function in R for this version of the test, and it is simply the t.test() function with the paired = TRUE argument. This version of the test is actually the standard version of the Student’s t-test with paired samples. Note that the alternative hypothesis is \(H_1: \mu_D > 0\) so we need to add the argument alternative = "greater" as well:
test <- t.test(dat5$after, dat5$before,
alternative = "greater",
paired = TRUE
)
test##
## Paired t-test
##
## data: dat5$after and dat5$before
## t = 4.4721, df = 4, p-value = 0.005528
## alternative hypothesis: true mean difference is greater than 0
## 95 percent confidence interval:
## 4.186437 Inf
## sample estimates:
## mean difference
## 8Note that we wrote after and then before in this order. If you write before and then after, make sure to change the alternative to alternative = "less".
If your data is in the long format, use the tilde ~:
dat5 <- data.frame(
value = c(9, 8, 1, 3, 2, 16, 11, 15, 12, 9),
time = c(rep("before", 5), rep("after", 5))
)
dat5## value time
## 1 9 before
## 2 8 before
## 3 1 before
## 4 3 before
## 5 2 before
## 6 16 after
## 7 11 after
## 8 15 after
## 9 12 after
## 10 9 aftertest <- t.test(value ~ time,
data = dat5,
alternative = "greater",
paired = TRUE
)
test##
## Paired t-test
##
## data: value by time
## t = 4.4721, df = 4, p-value = 0.005528
## alternative hypothesis: true mean difference is greater than 0
## 95 percent confidence interval:
## 4.186437 Inf
## sample estimates:
## mean difference
## 8The output above recaps all the information needed to perform the test (compare these results found in R with the results found by hand).
The p-value can be extracted as usual:
test$p.value## [1] 0.005528247The p-value is 0.006 so at the 5% significance level we reject the null hypothesis of the mean of the differences being equal to 0, meaning that we can conclude that the treatment is effective in increasing the running capabilities (because the mean of the differences is greater than 0). This result confirms what we found by hand.
Combination of plot and statistical test
After having written this article, I discovered the {ggstatsplot} package which I believe is worth mentioning here, in particular the ggbetweenstats() and ggwithinstats() functions for independent and paired samples, respectively.
These two functions combine a boxplot—representing the distribution for each group—and the results of the statistical test displayed in the subtitle of the plot.
See examples below for scenarios 2, 3 and 5. Unfortunately, the package does not allow to run tests for scenarios 1 and 4.
Scenario 2: Independent samples with 2 equal but unknown variances
The ggbetweenstats() function is used for independent samples:
# load package
library(ggstatsplot)
library(ggplot2)
# plot with statistical results
ggbetweenstats(
data = dat2bis,
x = sample,
y = value,
plot.type = "box", # for boxplot
type = "parametric", # for student's t-test
var.equal = TRUE, # equal variances
centrality.plotting = FALSE # remove mean
) +
labs(caption = NULL) # remove caption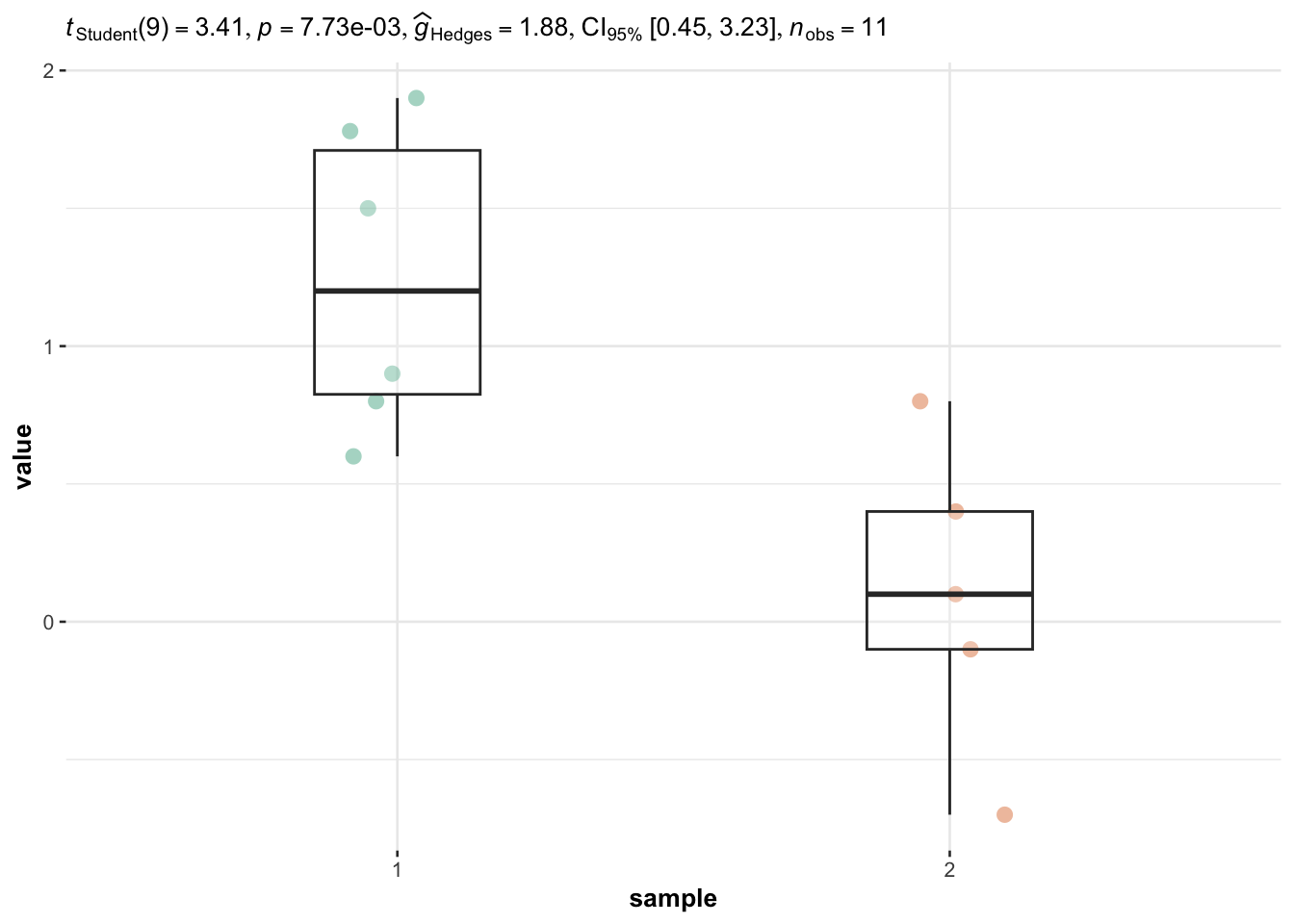
The p-value is displayed after p = in the subtitle of the plot. Based on this plot and the p-value being lower than 5% (p-value = 0.008), we reject the null hypothesis that the two population means are equal.
Note that, the p-value is two times as large as the one obtained with the t.test() function because when we ran t.test() we specified alternative = "greater" (i.e., a one-sided test). In our plot with the ggbetweenstats() function, it is a two-sided test that is performed by default, that is, alternative = "two.sided".
Scenario 3: Independent samples with 2 unequal and unknown variances
We also have independent samples so we use the ggbetweenstats() function again, but this time the two populations variances are not assumed to be equal so we specify the argument var.equal = FALSE:
# plot with statistical results
ggbetweenstats(
data = dat3,
x = sample,
y = value,
plot.type = "box", # for boxplot
type = "parametric", # for student's t-test
var.equal = FALSE, # unequal variances
centrality.plotting = FALSE # remove mean
) +
labs(caption = NULL) # remove caption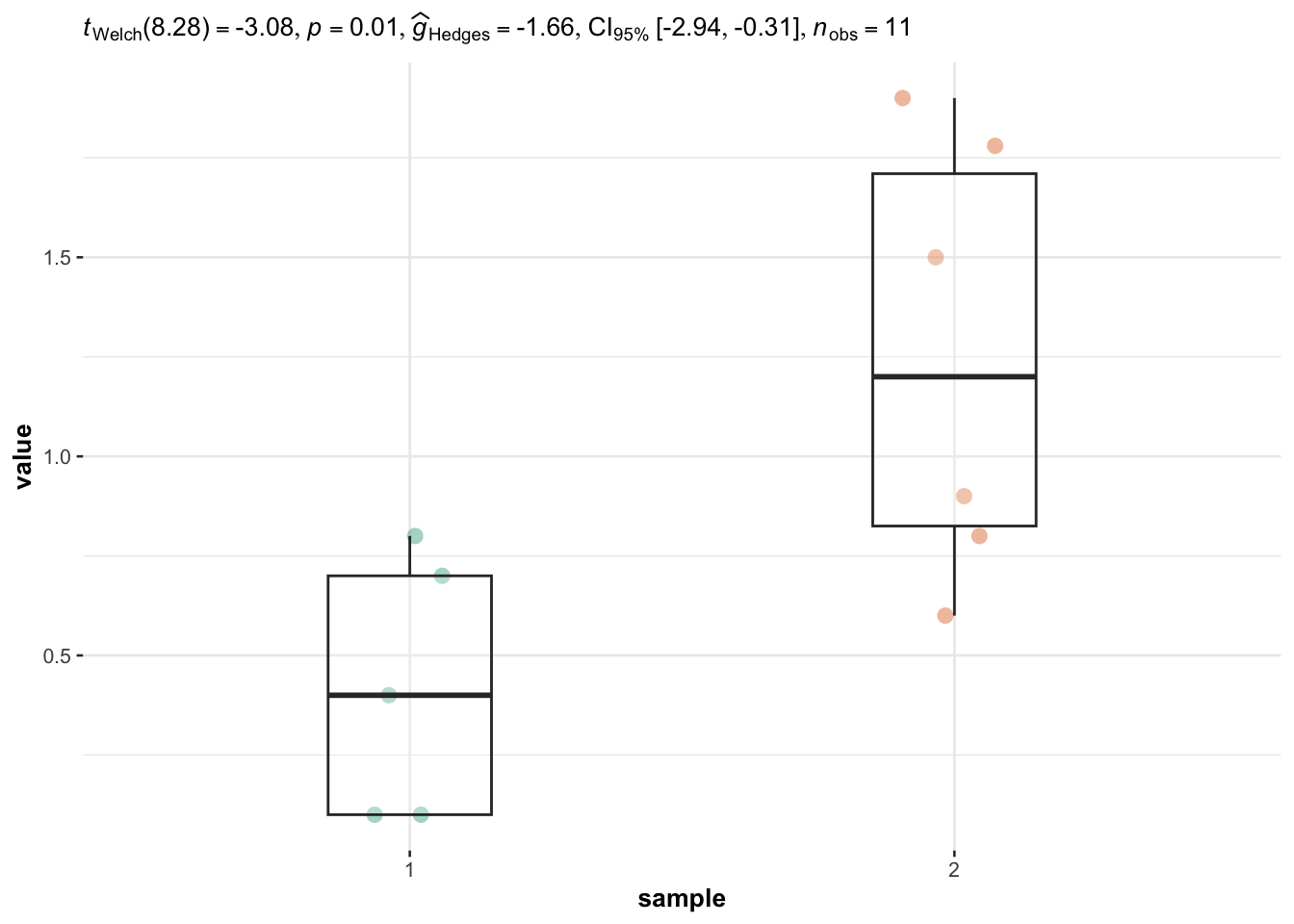
Based on the output, we reject the null hypothesis that the two population means are equal (p-value = 0.01).
Note that the p-value displayed in the subtitle of the plot is also two times larger than with the t.test() function for the same reason than above.
Scenario 5: Paired samples where the variance of the differences is unknown
In this case, the samples are paired so we use the ggwithinstats() function:
ggwithinstats(
data = dat5,
x = time,
y = value,
type = "parametric", # for student's t-test
centrality.plotting = FALSE # remove mean
) +
labs(caption = NULL) # remove caption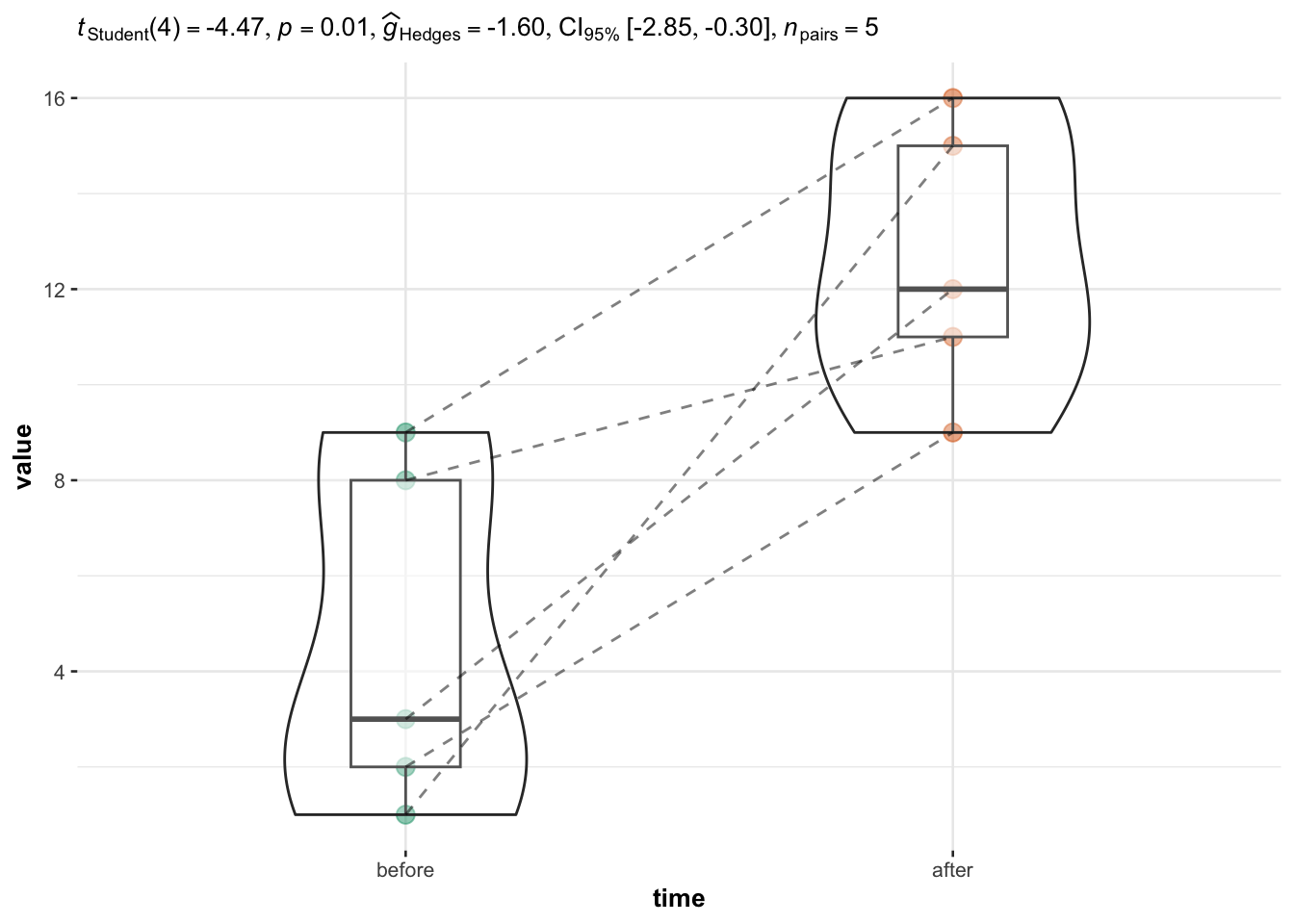
Based on the output, we reject the null hypothesis that mean of the differences between the two populations is equal to 0 (p-value = 0.01).
Again the p-value in the subtitle of the plot is twice the one obtained with the t.test() function for the same reason than above.
The point of this section was to illustrate how to easily draw plots together with statistical results, which is exactly the aim of the {ggstatsplot} package. See more details and examples in this article.
Assumptions
As for many statistical tests, there are some assumptions that need to be met in order to be able to interpret the results. When one or several of them are not met, although it is technically possible to perform these tests, it would be incorrect to interpret the results or trust the conclusions.
Below are the assumptions of the Student’s t-test for two samples, how to test them and which other tests exist if an assumption is not met:
- Variable type: A Student’s t-test requires a mix of one quantitative dependent variable (which corresponds to the measurements to which the question relates) and one qualitative independent variable (with exactly 2 levels which will determine the groups to compare).
- Independence: The data, collected from a representative and randomly selected portion of the population, should be independent between groups and within each group. The assumption of independence is most often verified based on the design of the experiment and on the good control of experimental conditions rather than via a formal test. If you are still unsure about independence based on the experiment design, ask yourself if one observation is related to another (if one observation has an impact on another) within each group or between the groups themselves. If not, it is most likely that you have independent samples. If observations between samples (forming the different groups to be compared) are dependent (for example, if two measurements have been collected on the same individuals as it is often the case in medical studies when measuring a metric (i) before and (ii) after a treatment), the paired version of the Student’s t-test, called the Student’s t-test for paired samples, should be preferred in order to take into account the dependency between the two groups to be compared.
- Normality:
- With small samples (usually \(n < 30\)), when the two samples are independent, observations in both samples should follow a normal distribution. When using the Student’s t-test for paired samples, it is the difference between the observations of the two samples that should follow a normal distribution. The normality assumption can be tested visually thanks to a histogram and a QQ-plot, and/or formally via a normality test such as the Shapiro-Wilk or Kolmogorov-Smirnov test. If, even after a transformation (e.g., logarithmic transformation, square root, etc.), your data still do not follow a normal distribution, the Wilcoxon test (
wilcox.test(variable1 ~ variable2, data = datin R) can be applied. This non-parametric test, robust to non normal distributions, compares the medians instead of the means in order to compare the two populations. - With large samples (usually \(n \ge 30\)), normality of the data is not required (this is a common misconception!). By the central limit theorem, sample means of large samples are often well-approximated by a normal distribution even if the data are not normally distributed (Stevens 2013). It is therefore not required to test the normality assumption when the number of observations in each group/sample is large.
- With small samples (usually \(n < 30\)), when the two samples are independent, observations in both samples should follow a normal distribution. When using the Student’s t-test for paired samples, it is the difference between the observations of the two samples that should follow a normal distribution. The normality assumption can be tested visually thanks to a histogram and a QQ-plot, and/or formally via a normality test such as the Shapiro-Wilk or Kolmogorov-Smirnov test. If, even after a transformation (e.g., logarithmic transformation, square root, etc.), your data still do not follow a normal distribution, the Wilcoxon test (
- Equality of variances: When the two samples are independent, the variances of the two groups should be equal in the populations (an assumption called homogeneity of the variances, or even sometimes referred as homoscedasticity, as opposed to heteroscedasticity if variances are different across groups). This assumption can be tested graphically (by comparing the dispersion in a boxplot or dotplot for instance), or more formally via the Levene’s test (
leveneTest(variable ~ group)from the{car}package) or via a F test (var.test(variable ~ group)). If the hypothesis of equal variances is rejected, another version of the Student’s t-test can be used: the Welch test (t.test(variable ~ group, var.equal = FALSE)). Note that the Welch test does not require homogeneity of the variances, but the distributions should still follow a normal distribution in case of small sample sizes. If your distributions are not normally distributed or the variances are unequal, the Wilcoxon test should be used. This test does not require the assumptions of normality nor homoscedasticity of the variances. - Outliers: An outlier is a value or an observation that is distant from the other observations. There should be no significant outliers in the two groups, or the conclusions of your t-test may be flawed. There are several methods to detect outliers in your data but in order to deal with them, it is your choice to either:
- use the non-parametric version (i.e., the Wilcoxon test)
- transform your data (logarithmic or Box-Cox transformation, among others)
- or remove them (be careful)
Conclusion
This concludes a relatively long article. Thanks for reading.
I hope this article helped you to understand how the different versions of the Student’s t-test for two samples work and how to perform them by hand and in R. If you are interested, here is a Shiny app to perform these tests by hand easily (you just need to enter your data and select the appropriate version of the test thanks to the sidebar menu).
Moreover, I invite you to read:
- this article if you would like to know how to compute the Student’s t-test but this time, for one sample,
- this article if you would like to compare 2 groups under the non-normality assumption, or
- this article if you would like to use an ANOVA to compare 3 or more groups.
As always, if you have a question or a suggestion related to the topic covered in this article, please add it as a comment so other readers can benefit from the discussion.
References
Remind that inferential statistics, as opposed to descriptive statistics, is a branch of statistics defined as the science of drawing conclusions about a population from observations made on a representative sample of that population. See the difference between population and sample.↩︎
For the rest of the present article, when we write Student’s t-test, we refer to the case of 2 samples. See one sample t-test if you want to compare only one sample.↩︎
It is a least the case for parametric hypothesis tests. A parametric test means that it is based on a theoretical statistical distribution, which depends on some defined parameters. In the case of the Student’s t-test for two samples, it is based on the Student’s t distribution with a single parameter, the degrees of freedom (\(df = n_1 + n_2 - 2\) where \(n_1\) and \(n_2\) are the two sample sizes), or the normal distribution.↩︎
Thanks gmacar for pointing it out to me.↩︎
Liked this post?
- Get updates every time a new article is published (no spam and unsubscribe anytime):



